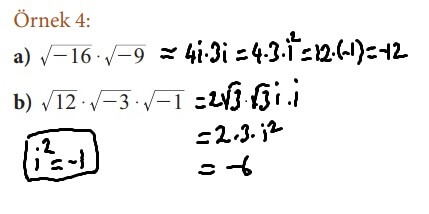Çarpanlara Ayırma ve Özdeşlikler Konu Anlatımı
ÇARPANLARA AYIRMA YÖNTEMLERİ VE ÖZDEŞLİKLER ÖRNEKLERLE KONU ANLATIMI
Çarpanlara ayırma ve özdeşlikler, matematiğin başta denklem çözümleri olmak üzere bir çok konu için olmazsa olmaz bir konusudur. Bu konuda eksiği olan 10.sınıf öğrencisi hem 11.sınıfta hem de 12.sınıf matematik konularında zorluk yaşayacaklardır. Zaten bu nedenle bu yıl, dersine girmiş olduğum 10.sınıflarda bu konuyu işlerken elimden gelen özeni göstermeye çalıştım. Bol bol test paylaşmaya çalıştım.
Çarpanlara ayırma ve özdeşlikler konusu matematiğin en temel konularından biri olup sınavlarda çokça karşımıza çıkar. Özellikle ikinci dereceli denklem çözümünde çok kullanılır. Aynı şekilde limit belirsizliklerini gidermek için çarpanlara ayırmadan yararlanılır. Özdeşliklerin kullanılmadığı konu matematikte neredeyse yok denilecek kadar azdır. Bu nedenle ÖZDEŞLİKLER ÇOK İYİ ÖĞRENİLMELİ. Konuyu daha iyi kavrayabilmek amacıyla bol bol soru çözmeli ve pratiğimizi artırmalıyız. Çözerken farklı bir bakış açısıyla bakmanız gereken bu konuda çokça soru tarzı ile karşılaşacaksınız. Bu da sizi farklı yollardan düşünmeye sevk edecek. Matematiğin amacı da sizde farklı bir düşünce yapısı oluşturmaktır. O zaman Çarpanlara ayırma ve özdeşlikler konumuza örneklerle başlayalım.
Özellikle, iki kare farkı, iki terimin toplamının-farkının karesi, iki terimin toplamının yada farkının küpü, küplerin toplamı-farkı özdeşlikleri matematiğin olmazsa olmaz özdeşlikleri olduğunu asla unutmayın
Çarpanlara ayırma ve özdeşlikler konu özetleri hem 10.sınıf matematik sınavlarına hem de YKS; TYT-AYT,KPSS, DGS gibi sınavlara hazırlanan öğrencilerin çok işine yaracağını ümit ediyor.Sizleri konu özetleri ile baş başa bırakıyoruz.
Çarpanlara Ayırma Yöntemleri
Tabi her ifade çarpanlarına ayrılamaz. Tıpkı 5,7,19.. asal sayılar gibi.
Asal Polinom
Sabit olmayan ve birden fazla polinomun çarpımı biçiminde yazılamayan polinomlara indirgenemeyen polinomlar denir.
Sabit olmayan, baş katsayısı 1 olan ve kendisinden küçük dereceli polinomların çarpımı olarak yazılamayan polinomlara asal polinom denir.
Bir polinomu iki ya da daha çok polinomun çarpımı biçiminde yazma işlemine bu polinomu çarpanlarına ayırma işlemi denir. Şimdi örneklerle çarpanlara ayırma ve özdeşlikler konusunu özetleyelim.
Bir ifade çarpanlarına ayrılırken ilk akla ortak çarpan parantezine alınıp alınmadığına bakılmalı.Eğer ortak çarpan yoksa diğer yöntemler düşünülmeli.Ortak çarpan parantezi ile çarpanlara ayırırken, çarpmanın toplamad yada çıkarma işlemi üzerine dağılma özelliğinden yararlanılır.
Bir polinomun ya da bir cebirsel ifadenin terimlerinde ortak çarpanlar varsa ortak çarpanların en küçük üstlerinin çarpımı, bu polinomun her teriminin ortak çarpanıdır.
1. Ortak çarpan parantezine alma:
2. Gruplandırarak Çarpanlara Ayırma
Verilen polinomun bütün terimlerinin ortak çarpanı bulunmayabilir. Ancak, polinomun terimlerini belirli gruplara ayırarak ortak çarpanlar bulabiliriz. Her gruptan elde edilen çarpanlar arasında ortak olanlar varsa, bu yöntem kolayca uygulanabilir.
Verilen ifadenin her teriminde ortak çarpan yoksa ortak çarpanı olan terimler kendi aralarında gruplandırılarak ortak çarpan parantezine alınır
Aşağıdaki örnek gibi sorularda bu iki kural çok önemli hale geliyor.
3.Özdeşlikler:
Bilinmeyenlere verilen her sayı değeri için sağlanan eşitliklere özdeşlik denir.
Örnek:
Bir çok ifadeyi çarpanlarına ayırmak için özdeşliklerden yararlanılır. Önemli özdeşliklerden bazılarını sırayla ele alalım.
özdeşliğine iki kare farkı özdeşliği denir. İki terimin toplamı ile farkının çarpımı, birinci terimin karesi ile ikinci terimin karesinin farkına eşittir. Bu özdeşlik o kadar önemli ki; bu formülü bilmeyen matematik bilmiyor desek haksız olmayız. Çalışma odasının duvarlarına yazılmayı hak eden çok önemli bir matematik kuralıdır.
özdeşliğine iki terim toplamının karesi özdeşliği (tam kare özdeşliği) denir.İki terim toplamının karesi alınırken; birinci terimin karesi, birinci ile ikinci terim çarpımının iki katı, ikinci terimin karesi alınıp toplanır.
özdeşliğine iki terim farkının karesi özdeşliği (tam kare özdeşliği) denir.İki terim farkının karesi alınırken; birinci terimin karesi ile ikinci terimin karesi toplamından, birinci terim ile ikinci terim çarpımının iki katı çıkarılır.
İki terim toplamının veya farkının küp özdeşliği; pascal üçgeni yada binom açılımı ile bulunur. Her ikisi de 3+1=4 terimden oluşur. İlk ve son terimde birinci ve ikinci terimin küpleri yer alır.İki terimin farkının küpü, iki terimin toplamının küpünün +, -, +, – şeklinde yazılmış halidir.Bu nedenle ilk özdeşliği ezberleyen, böylece ikincisini de ezberlemiş olur.
İki terim toplamının veya farkının küp özdeşliklerine birinci ve sonuncu terim yalnız bırakılıp diğer iki terim diğer tarafa atılır, ortak çarpan parantezine alınca iki terimin küplerinin toplamı ve farkı özdeşlikleri ortaya çıkar.Bu iki özdeşlik daha ziyade çarpanlara ayırmada kullanılır.
f . Tam Kare Özdeşliğinden Yararlanarak Çarpanlara Ayırma
özdeşliklerinden yararlanarak yapılan çarpanlara ayırmadır.İki terim toplamının karesi özdeşliği üç terimlidir. Üç terimli bir ifadede iki terimin karekökü alınabiliyor ve üçüncü terimi de bu iki karekökün çarpımının iki katından elde edilebiliyorsa bu ifade bir tam kare olarak yazılabilir.
1. ve 3. terimler pozitif ise karekökleri alınır. Kareköklerin çarpımının 2 katı 2. terimi veriyorsa, ifade tam karedir. Tam karenin işareti 2. terimin işaretidir.
6. Değişken değiştirme yöntemi:
Değişken değiştirme yönteminde, verilen İfadedeki değişkenin ya da belli bir ifadenin yerine yeni bir değişken yazılarak verilen ifade sade hale getirilir. Sade hale gelmiş ifade çarpanlarına ayrılır.
Değişken değiştirme daha ziyade derecesi karenin katları olan dördüncü, altıncı dereceli ifadelerde kullanılır. X^2=k X^3=m gibi değişken kullanılarak ifade ikinci dereceli hale getirilip yukarıdaki yöntemlerden biri ile işlem sonuçlandırılır.Aslında değişken değiştirme sadece çarpanlara ayırmada değil matematikte bir çok konuda kullanılır.İntegralde olduğu gibi.
Rasyonel İfadelerde Sadeleştirme
Rasyonel ifadenin payı ve paydası ayrı ayrı çarpanlarına ayrılır. Pay ve paydadaki ortak çarpanlar sadeleştirilir.
Böylece bol bol örneklerle çarpanlara ayırma yöntemlerini, özdeşlikleri özetlemiş olduk. Şimdi sizlerin yapacağı bu konuda bol bol soru çözerek konuyu en güzel şekilde pekiştirmek olmalıdır. Matematikte başarının en temel kurallarından biri de bol bol soru çözmek olduğunu tekrar söylemeye gerek yok sanırım.
Ali SANCI-Matematik Öğretmeni
Hepinize Başarılar Diliyoruz!
10.Sınıf Matematik Karmaşık Sayılar Örneklerle Konu Anlatımı-Özeti
10.Sınıf matematik ikinci dereceden denklemler konusunun alt başlıklarından biri de “Karmaşık sayılar” dır.
a ≠ 0 ve a, b, c d R olmak üzere ax^2 + bx + c = 0 denkleminde ∆ = b^2 – 4ac < 0 ise bu denklemin R de (gerçek sayılar) çözüm kümesi boş kümedir. Bu durumda, denklemin köklerinin bulunabilmesi için gerçek sayılar kümesini de kapsayan yeni bir sayı kümesine ihtiyaç duyuldu, bu yeni sayı kümesine karmaşık sayılar kümesi denmiştir. Karmaşık sayılar kümesi C sembolü ile gösterilir.
a, b birer reel sayı, i sanal sayı birimi i^2=1 olmak üzere z = a + bi şeklindeki sayılara karmaşık sayılar denir.
a ya karmaşık sayının gerçek kısmı denir ve Re(z) = a şeklinde, b ye ise sanal (imajiner) kısmı denir ve İm(z) = b şeklinde gösterilir.
Karmaşık sayılar konusu, en son müfredat değişikliği ile oldukça sade hale getirildi. Ancak hala kaynakların bir çoğunda konu çok ayrıntılı ele alınıyor. Müfredatta olmayan karmaşık sayılarda işlemlerle ilgili sorulara yer veriliyor. Aşağıdaki eklemiş olduğum genel tarama soru testini farklı kaynaklardan derlerken yeni müfredatın dışına çıkmamaya özen gösterdim.
10.Sınıf matematik dersi “İkinci dereceden denklemler-karmaşık sayılar” müfredatı şu şekilde yer almaktadır. 2020-2021 yılı 10.sınıf okuyan öğrenciler 2023 YKS sınavında, müfredata göre karmaşık sayıların bu kadarından sorumlu olacaklar.
Yukarıda da görüldüğü gibi karmaşık sayılarda eşlenik dışında, karmaşık sayıların eşitliği ve karmaşık sayılarda dört işlem konusu işlenmeyecek. Bu nedenle karmaşık sayılar konusunu burada özetlerken, ders kitaplarındaki anlatımı göz önüne alacağım.
10.Sınıf Matematik Karmaşık Sayılar Örneklerle Konu Özeti-Konu Anlatımı
1- Karmaşık sayı ve karmaşık sayının reel ve sanal kısmı,
z = a + bi şeklindeki sayılara karmaşık sayılar denir ve bu sayıdaki a ya karmaşık sayının gerçek kısmı denir ve Re(z) = a şeklinde, b ye ise sanal (imajiner) kısmı denir ve İm(z) = b şeklinde gösterilir.
2- Sanal Birimin kuvvetleri,
3- Karmaşık sayının eşleniği,
a ve b birer reel sayı olmak üzere z = a + bi karmaşık sayısının sanal kısmının işareti değiştirilerek oluşturulan a – bi karmaşık sayısına a + bi karmaşık sayısının eşleniği denir ve bu 
ile gösterilir.
a,b,c birer reel sayı olmak üzere ax^2 + bx + c = 0 ikinci dereceden bir bilinmeyenli denkleminde diskriminant(delta) değeri sıfırdan küçükse denklemin sanal iki farklı kökler vardır. Ve bu kökler bir birinin eşleniğidir.
Bu kökler şu formüllerle bulunur:
10.Sınıf matematik karmaşık sayılar genel tarama soruları ve cevapları için TIKLAYINIZ
YouTube
Kunduz Dönemlik İndirim Kodu
