Home » Search results for 'eba' (Page 17)
Search Results for: eba
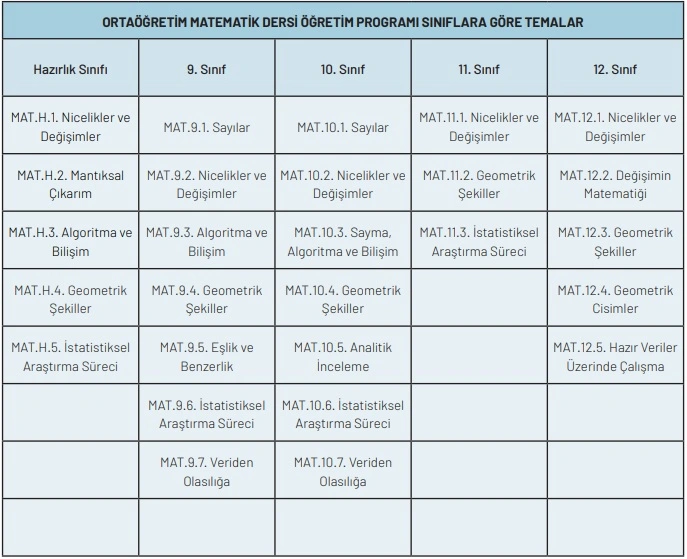
9,10,11 ve 12.Sınıf Matematik Konuları (2024 Müfredat programına göre)
“Türkiye Yüzyılı Maarif Modeli” adını alan yeni müfredat programı onaylandı. Yeni öğretim programları 2024-2025 eğitim öğretim yılında 9.sınıflardan başlanarak kademeli uygulanacak. MEB konuların %35 sadeleştirildiğini belirtti. Böyle olunca diğer dersler gibi lise matematik dersi de bundan nasibini aldı. Belki de en ciddi değişiklik matematikte olmuştur, emin değilim bu konuda. Bazı konular tamamen çıkarılırken (integral gibi) , bazı konuların bir kısmı (trigonometri gibi) çıkarıldı. Bazı konuların sınıflar düzeyinde yer değişiklikleri oldu. Örneğin polinomlar konusu 10.sınıfta işleniyorken yeni programda 12.sınıfta işlenecek. Bunun gibi değişikliğe epey örnek verilebilir. Bunları aşağıdaki konu listelerinde de görebilirsiniz.
Geometri konuları tüm sınıflara dağıtılmış. Daha önceki programda 10.sınıfta yer alan çokgenler-dörtgenler 11.sınıfa, 10.sınıfa ise 9.sınıf konularından olan üçgenin yardımcı elemanları ve üçgenin alanı alınmış. 12.sınıfta işlenen çemberin analitiği tamamen çıkarılarak yerine 11.sınıfta işlenen çember-daire konu taşınmış.
9.Sınıf Matematik Konuları (İlk kez 2024-2025 yılında okutulmaya başlanacak)
9.Sınıfta en çok ders saati (36) ve yüzde oranı (%17) en fazla olan konular: Sayılar, eşlik ve benzerlik
1.Ünite: Sayılar
2.Ünite: Nicelikler ve Değişimler
3.Ünite: Algoritma ve Bilişim
4.Ünite: Geometrik Şekiller
5.Ünite: Eşlik ve Benzerlik
6.Ünite: İstatistiksel Araştırma Süreci
7.Ünite: Veriden Olasılığa
2024-2025 Yılı 9.Sınıf Matematik Konuları – Yeni (Kazanımlar da var…)
10.Sınıf Matematik Konuları (İlk kez 2025-2026 yılında okutulmaya başlanacak)
Sayılar
EBOB, EKOK
Nicelikler ve Değişimler
Fonksiyonlar
Sayma, Algoritma ve Bilişim:
Sayma Stratejileri, Cebirsel ve Fonksiyonel İşlemlerin Algoritmik Yapısı
Geometrik Şekiller:
Dik Üçgende Trigonometrik Oranlar ve Trigonometrik Özdeşlikler
Üçgende Yardımcı Elemanlar ve Bunlar Arasındaki İlişkiler
Üçgende Alan,
Sinüs ve Kosinüs Teoremleri
Analitik İnceleme:
Dik Koordinat Sisteminde Nokta ve Doğrunun Analitik İncelenmesi
İki Nokta Arasındaki Uzaklık
Bir Doğru Parçasını Belli Bir Oranda Bölme
İstatistiksel Araştırma Süreci:
İki Kategorik Değişkenin İlişkiliğini İçeren İstatistiksel Problemi Oluşturma
Verileri Toplama ve Analize Hazır Hâle Getirme
Bulgulara Ulaşma ve Bulguları Yorumlama
Veriden Olasılığa:
Olasılık
11.Sınıf Matematik Konuları (İlk kez 2026-2027 yılında okutulmaya başlanacak)
En çok ders saati (62) ve yüzde oranı %27 olan konu: Geometrik şekiller (Çokgenler-dörtgenler)
Nicelikler ve Değişimler:
Trigonometri
Logaritma
Fonksiyonlarla Dört İşlem ve Fonksiyonların Bileşkesi
Geometrik Şekiller:
Dörtgenler
Çokgenler
İstatistiksel Araştırma Süreci
12.Sınıf Matematik Konuları (İlk kez 2027-2028 yılında okutulmaya başlanacak)
Yeni programda integral çıkarıldı ancak, limit ve türev daha kapsamlı ele alındı.
Nicelikler ve Değişimler:
Gerçek Sayı Dizileri
Aritmetik ve Geometrik Diziler
Polinomlar
Değişimin Matematiği:
Limit ve Süreklilik
Ortalama Değişim Oranı, Anlık Değişim Oranı
Türev
Türevin Geometrik Yorumu ve Türev Uygulamaları
Geometrik Şekiller:
Çember ve Daire
Hazır Veriler Üzerinde Çalışma:
Veri Bilim ve İstatistik
2027 YKS sınavlarında sorular yeni müfredat konularından çıkacak
Ve 2027-2028 eğitim öğretim yılı sonunda yapılacak 2028 YKS sınavında sorular 2024 yılında yayınlanan yeni müfredat programındaki yukarıdaki konulardan soru çıkacak.
2025, 2026 ve 2027 YKS sınavları önceki konulara göre yani 2018 tarihli öğretim programındaki konulardan soru sorulacak.
İlkokul-Ortaokul-Lise Müfredat Programı (2024)
Lise Hazırlık, 9, 10 ,11 ve 12.Sınıf Yeni Matematik Müfredat Programı için TIKLAYIN
Ortaokul 5, 6 ,7 ve 8.Sınıf Yeni Matematik Müfredat Programı için TIKLAYIN
İlkokul 1, 2 ,3 ve 4.Sınıf Yeni Matematik Müfredat Programı için TIKLAYIN
10.Sınıf Matematik Karmaşık Sayılar Örneklerle Konu Anlatımı-Özeti
10.Sınıf matematik ikinci dereceden denklemler konusunun alt başlıklarından biri de “Karmaşık sayılar” dır.
a ≠ 0 ve a, b, c d R olmak üzere ax^2 + bx + c = 0 denkleminde ∆ = b^2 – 4ac < 0 ise bu denklemin R de (gerçek sayılar) çözüm kümesi boş kümedir. Bu durumda, denklemin köklerinin bulunabilmesi için gerçek sayılar kümesini de kapsayan yeni bir sayı kümesine ihtiyaç duyuldu, bu yeni sayı kümesine karmaşık sayılar kümesi denmiştir. Karmaşık sayılar kümesi C sembolü ile gösterilir.
a, b birer reel sayı, i sanal sayı birimi i^2=1 olmak üzere z = a + bi şeklindeki sayılara karmaşık sayılar denir.
a ya karmaşık sayının gerçek kısmı denir ve Re(z) = a şeklinde, b ye ise sanal (imajiner) kısmı denir ve İm(z) = b şeklinde gösterilir.
Karmaşık sayılar konusu, en son müfredat değişikliği ile oldukça sade hale getirildi. Ancak hala kaynakların bir çoğunda konu çok ayrıntılı ele alınıyor. Müfredatta olmayan karmaşık sayılarda işlemlerle ilgili sorulara yer veriliyor. Aşağıdaki eklemiş olduğum genel tarama soru testini farklı kaynaklardan derlerken yeni müfredatın dışına çıkmamaya özen gösterdim.
10.Sınıf matematik dersi “İkinci dereceden denklemler-karmaşık sayılar” müfredatı şu şekilde yer almaktadır. 2020-2021 yılı 10.sınıf okuyan öğrenciler 2023 YKS sınavında, müfredata göre karmaşık sayıların bu kadarından sorumlu olacaklar.
Yukarıda da görüldüğü gibi karmaşık sayılarda eşlenik dışında, karmaşık sayıların eşitliği ve karmaşık sayılarda dört işlem konusu işlenmeyecek. Bu nedenle karmaşık sayılar konusunu burada özetlerken, ders kitaplarındaki anlatımı göz önüne alacağım.
10.Sınıf Matematik Karmaşık Sayılar Örneklerle Konu Özeti-Konu Anlatımı
1- Karmaşık sayı ve karmaşık sayının reel ve sanal kısmı,
z = a + bi şeklindeki sayılara karmaşık sayılar denir ve bu sayıdaki a ya karmaşık sayının gerçek kısmı denir ve Re(z) = a şeklinde, b ye ise sanal (imajiner) kısmı denir ve İm(z) = b şeklinde gösterilir.
2- Sanal Birimin kuvvetleri,
3- Karmaşık sayının eşleniği,
a ve b birer reel sayı olmak üzere z = a + bi karmaşık sayısının sanal kısmının işareti değiştirilerek oluşturulan a – bi karmaşık sayısına a + bi karmaşık sayısının eşleniği denir ve bu 
ile gösterilir.
a,b,c birer reel sayı olmak üzere ax^2 + bx + c = 0 ikinci dereceden bir bilinmeyenli denkleminde diskriminant(delta) değeri sıfırdan küçükse denklemin sanal iki farklı kökler vardır. Ve bu kökler bir birinin eşleniğidir.
Bu kökler şu formüllerle bulunur:
10.Sınıf matematik karmaşık sayılar genel tarama soruları ve cevapları için TIKLAYINIZ
YouTube
Kunduz Dönemlik İndirim Kodu
