10.Sınıf matematik ikinci dereceden denklemler konusunun alt başlıklarından biri de “Karmaşık sayılar” dır.
a ≠ 0 ve a, b, c d R olmak üzere ax^2 + bx + c = 0 denkleminde ∆ = b^2 – 4ac < 0 ise bu denklemin R de (gerçek sayılar) çözüm kümesi boş kümedir. Bu durumda, denklemin köklerinin bulunabilmesi için gerçek sayılar kümesini de kapsayan yeni bir sayı kümesine ihtiyaç duyuldu, bu yeni sayı kümesine karmaşık sayılar kümesi denmiştir. Karmaşık sayılar kümesi C sembolü ile gösterilir.
a, b birer reel sayı, i sanal sayı birimi i^2=1 olmak üzere z = a + bi şeklindeki sayılara karmaşık sayılar denir.
a ya karmaşık sayının gerçek kısmı denir ve Re(z) = a şeklinde, b ye ise sanal (imajiner) kısmı denir ve İm(z) = b şeklinde gösterilir.
Karmaşık sayılar konusu, en son müfredat değişikliği ile oldukça sade hale getirildi. Ancak hala kaynakların bir çoğunda konu çok ayrıntılı ele alınıyor. Müfredatta olmayan karmaşık sayılarda işlemlerle ilgili sorulara yer veriliyor. Aşağıdaki eklemiş olduğum genel tarama soru testini farklı kaynaklardan derlerken yeni müfredatın dışına çıkmamaya özen gösterdim.
10.Sınıf matematik dersi “İkinci dereceden denklemler-karmaşık sayılar” müfredatı şu şekilde yer almaktadır. 2020-2021 yılı 10.sınıf okuyan öğrenciler 2023 YKS sınavında, müfredata göre karmaşık sayıların bu kadarından sorumlu olacaklar.

Yukarıda da görüldüğü gibi karmaşık sayılarda eşlenik dışında, karmaşık sayıların eşitliği ve karmaşık sayılarda dört işlem konusu işlenmeyecek. Bu nedenle karmaşık sayılar konusunu burada özetlerken, ders kitaplarındaki anlatımı göz önüne alacağım.
10.Sınıf Matematik Karmaşık Sayılar Örneklerle Konu Özeti-Konu Anlatımı
1- Karmaşık sayı ve karmaşık sayının reel ve sanal kısmı,
z = a + bi şeklindeki sayılara karmaşık sayılar denir ve bu sayıdaki a ya karmaşık sayının gerçek kısmı denir ve Re(z) = a şeklinde, b ye ise sanal (imajiner) kısmı denir ve İm(z) = b şeklinde gösterilir.



2- Sanal Birimin kuvvetleri,

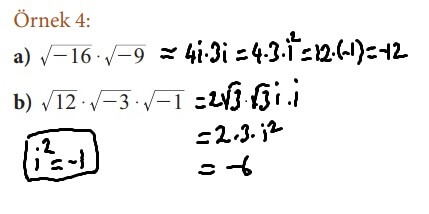



3- Karmaşık sayının eşleniği,
a ve b birer reel sayı olmak üzere z = a + bi karmaşık sayısının sanal kısmının işareti değiştirilerek oluşturulan a – bi karmaşık sayısına a + bi karmaşık sayısının eşleniği denir ve bu ![]() ile gösterilir.
ile gösterilir.

a,b,c birer reel sayı olmak üzere ax^2 + bx + c = 0 ikinci dereceden bir bilinmeyenli denkleminde diskriminant(delta) değeri sıfırdan küçükse denklemin sanal iki farklı kökler vardır. Ve bu kökler bir birinin eşleniğidir.
Bu kökler şu formüllerle bulunur:
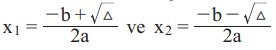


10.Sınıf matematik karmaşık sayılar genel tarama soruları ve cevapları için TIKLAYINIZ